疫苗的 昏昏倒地 Debuff 下，云完了前四题就去美化了

# CF1534

# A

题意：

$n\times m$ 的字符矩阵，只含字符 R W . ，要把所有 . 的地方换成 R W ，要求 R 上下左右不是 R ， W 同样的要求。

$$n\le100$$

题解：

发现一个点即可把所有的地方染好色

$n$ 很小，暴力染色即可。

注意初始没有一个色的时候。

这种 sb 题要注意认真检查每一步的细节，不要翻车。

# B

题意：

给定 $n$ 列的直方图，每列有个高度 $d_i$ ，一个图的丑陋度为裸露在外的竖线长度和，如：

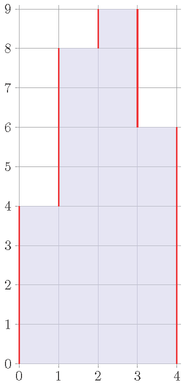
每次可把一个地方高度减一，最小化 操作数+丑陋度 和。

题解：

简单考虑贡献法贪心

容易发现若一列高于旁边两列，削它每次 操作数+1 丑陋度-2 ，这样是优的，而削到与两边较大的那列相同高度时贡献会减小。

注意特判边界情况

# C

题意：

给出 $2\times n$ ，每行是个排列，可以交换一列两个元素，要求经过操作后没有相同元素在同一行的数阵有多少个。

$$n\le 4\times 10^5$$

题解：
对于每一个列连入一个并查集中，最后答案为 $2^c$ ，$c$ 为联通块数量。

由于相同的数字不能在同一行，这又是两个排列，这样一来，我们一个联通块中，一列翻了之后其余都要做相应的转换，于是就有翻不翻两种情况。

# D

题意：

交互题，一棵树，可进行不超过 $\lfloor{n\over 2}\rfloor$ 次询问，每次询问一个 $x$ ，返回 $n$ 个数，表示每个点到 $x$ 的距离，还原树的结构。

题解：
先随便问个点 $x$ ，得到的距离中，$1$ 的就是与他相邻的，我们把距离为奇数点或偶数点中选出较小的那个集合，问一遍就做完了。

可以发现奇数点或偶数点集合中较小的那个一定是小于 $\lfloor{n\over 2}\rfloor$ 的。

# P $\color{red}E$

题解：

​ 交互题，长度为 $n$ 的序列与 $k$ ，每次可询问 $k$ 个数字 $x_1\dots x_k$，返回 $a_{x_1}\oplus a_{x_2} \dots \oplus a_{x_k}$ 。求 $a_1\oplus a_2 \dots \oplus a_n$

题解：
我们并不关心每个 $a$ 具体是多少，于是可以看做翻牌子，每次可翻 $k$ 个牌子，求最终每个牌子被翻奇数次的方案。

​ 设每个地方被翻 $b_i$ 次，我们要求：

$$k | \sum b \\ \forall i\in[1,n], b_i \& 1 = 1$$

​ 此时操作了 ${\sum b\over k}=x$ 次，于是 $b_{max} \le x$ ，然后构造出 $b$ ，先赋每个 $b_i$ 为 $1$ ，每次加 $2$ 。为什么这样有解？不会证明，当然得首先特判掉 $n$ 为奇数且 $k$ 为偶数的情况，接下来就对了？？？？？

# F1

题意：
一个 $n\times m$ 的方格，有些地方有沙子，干扰一块沙子能使从这块沙子到最底下的路径中，擦到的沙子都掉下来，求最少干扰的沙子数。

$$n\times m\le 4\times 10^5$$

题解：
把一个点向所有他能干扰得到的，最上边的沙子连边，跑缩点，找入度为 $0$ 的点即可。

# F2

题意：

上题的基础上，每列有个 $a_i$ ，要求每列至少掉 $a_i$ 个沙子的最小干扰数。

题解：
把每列从下到上第 $a_i$ 个沙子称作关键点，则只要这一块掉下来就可以了。

先把关键点能到的其他关键点删掉，它不配，只要删掉之前关键点，这一块自然会掉。

可以发现缩点后每个点干扰后能影响的关键点是一段连续的区间，简单证明下，假设 $i<j<k$ 列中第 $i$ 列的点能够影响到 $k$ 列中关键点，却不能影响 $j$ 列中的关键点，那 $i$ 一连串影响到 $k$ 的链中在 $j$ 列一定有个点，在 $j$ 列关键下面，那 $j$ 也可以走这条链影响到 $k$ ，于是这样的第 $k$ 列关键点就在之前被 $j$ 列关键点吃掉了，它不配作为关键点。

所以可以通过反拓扑的方法求出每个点能够影响到的关键点左右端点，此时相当于要求一个最小线段数覆盖整个区间，简单贪心即可：把线段按左端点从小到大为第一关键字，右端点从大到小为第二关键字，排序。每次处理到 $i$ 表示把 $1\to i$ 区间全部覆盖完消耗的最小线段数，用个左端点在 $i$ 以内的，能推到的最远 $r$ 更新即可。

参考代码

1
2
3
4
5
6
7
8
9

sort(seg, seg + scnt, [](const pii &a, const pii &b) { return a.fi == b.fi ? a.se > b.se : a.fi < b.fi; });
	int Ans = 0;
	for (int i = 1, j = 0, rcur = 0, rr = 0; i <= covercnt; ++i) {
		while (j < scnt && seg[j].fi <= i) {
			if (seg[j].se > rcur) rcur = seg[j].se;
			++j;
		}
		if (i > rr) Ans++, rr = rcur;
	}

# G

题意：
平面直角坐标系上有 $n$ 个点要被处理，在 $(a,b)$ 点处理点 $(x,y)$ 的代价是 $\max\{|a-x|,|b-y|\}$ ，从 $(0,0)$ 出发，每次可向上 $or$ 向左走一步，求处理掉所有点的最小代价。

$$n\le 8\times 10^5 ,x,y\le 10^9$$

题解：

首先这个切比雪夫距离的代价并不好处理，所以使用一个经典我刚会的套路，把坐标 $(x,y)$ 转换成 $(x+y,x-y)$ ，此时切比雪夫距离就变成了曼哈顿距离，还带有一个 $1\over2$ 的常数，这个最后把求出的 $Ans$ 除以 $2$ 即可。

这个操作相当于是把坐标系顺时针旋转了 $45^\circ$ ，所以向右向上的移动变成了 $(x,y)\to (x+1,y) / (x+1,y+1)$ 这样斜着走，不难发现一个关键点 $(a,b)$ 在 $x=a$ 时处理是最优的，于是把关键点按转换后的坐标排序后可以得出一个 $dp$ ，设 $dp_{i,j}$ 表示处理到 $(i,j)$ 的最小代价，有转移:

$$dp_{i,j}=\min\limits_{b\in[j-|i-a|,j+|i-a|]} dp_{a,b} + \sum\limits_{(x,y),x=i}|y-j|$$

这个 $\min$ 下面的限制意思是从 $(a,b)$ 可以走到 $(i,j)$。

定义 $|x|$ 为值域大小，这个 $dp$ 的复杂度是 $\mathrm O(n|x|)$ ，于是我们要采用一种神奇的操作把复杂度变成 $\mathrm O(n\log n)$ ，这个操作被叫做 slope trick ，可以上 $\texttt{CF}$ 学习。

对于此题来说，我们把 $dp_{i,[]}$ 看做一个函数 $dp_i(x)$ ，把 $dp_{a,[]}$ 也看成一个函数 $g_a(x)$ ，$dp$ 方程就可以写成 $dp_i(x)=\min\limits_{b\in[j-|i-a|,j+|i-a|]}g_a(x) + |x-y_i|$ 的形式，对于每个转移来说，$y_i$ 是固定的，所以可以看成一个常数，相当于是将一个区间$\min$ 函数与一个绝对值函数合并得到一个新的函数 $dp_i(x)$ 。

观察这些函数的性质，发现 $|x-y_i|$ 是一个凸函数，只有一个转折点 $x=y_i$ ，而 $g(x),dp(x)$ ，都是由一连串的 $|x-y_j|$ 合并而来的，是一个分段函数，有一些转折点，且也是一个凸函数（斜率递增），这题要求我们做两种操作：1. 在 $[l,r]$ 中找到最小值。 2. 合并两个凸函数。

最小值显然会在斜率等于 $0$ 处取得，但这个位置不一定满足在 $[l,r]$ 中，于是我们用一个大根堆 $L$ 来维护这个分段函数斜率小于 $0$ 的那一段的每个转折点，每个转折点表示我们的函数在这个转折点处斜率加 $1$ ，所以若斜率在一个转折点 $u$ 处 $+x$ 则在优先队列中放 $x$ 个转折点 $u$ ，类似的，用一个小根堆 $R$ 来维护分段函数斜率大于 $0$ 的每个转折点。

利用一点初中数学知识，每次若 $r\le L$ 则最小值在 $L$ 处取得，若 $l \ge R$ 则最小值在 $R$ 处取得，若在 $[L,R]$ ，则直接取最小值。

还要求合并一个函数 $|x-y_i|$ ，相当于是与一个转折点集合 $s=\{y_i,y_i\}$ 取并，像上面一样讨论一下新转折点该放在哪边，还有一些旧的转折点因为增添了新转折点斜率发生了更改，所以分类讨论把 $L$ 的最大值移动到 $R$ 或 $R$ 的最小值移动到 $L$ 。

还有一道与这题类似的 slope trick 优化 $dp$ 的题 ，可以去做一做。