赛时做了 T2,想着 T1 是个大贪心 / Dp 不好写,T3 不会做就一直在做 T4,然后并没有发现 T4 是构造题。。。
做题的时候不要畏难,一些看上去不好写的东西想清楚细节再写基本不会写锅,但做法假了当然就。。。
# Solutions
# tree
给出一棵树,每次操作挑选联通的两个叶子把他们路径上边全删掉,求最小操作次数使得不能再操作。
贪心地考虑每棵子树内未匹配,可用的叶子数量。
根据奇偶性,可用的叶子数量只可能为 ,其他的叶子都在当前被操作掉了,然后就硬贪心。
# gcd
给定 个数字,每次可以把一个数字
+1或-1。求至多多少次操作能使得整个序列都为正数并且
答案的上界显然是 ,因为我们把每个数变成偶数就有一个 的公因子了。
然后我们惊讶的得出一个十分喵喵的结论:至多有 个数字被操作次数超过 这是咋想到的
换句话说,每个数字被操作次数超过 的概率是
所以对于每个数字 ,有 的概率至多被操作次数为 ,然后枚举 , , 的因子作为答案,暴力搞一遍后,没找到最终答案 的概率为 ,如果你比较欧,做个 30 次就差不多行了。
# game
Bob 陪 Alice 玩游戏,Alice 会构造一棵每个节点度数不超过 的带标号树,然后 Bob 选择两个节点把其路径按顺序抠出来,节点标号记做序列 ,Alice 会选出一个位置 把它后面全翻转再加上 或者 取负再加上
若最终这个序列是单调递增的,那么 Alice 胜利,否则 Bob 胜利
统计所有可能的游戏数目。
首先,每个人都是按最优策略决策的,而树是 Alice 构造的,所以这棵树满足无论 Bob 选哪里,Alice 都能赢。
所以叫 bob 陪 alice 玩游戏 然后 Alice 其实是个大美女,Bob 输了游戏赢了人生
手玩一下发现性质,单调或单峰的序列 Alice 能赢,这里借用一下 bigmurmur 的图
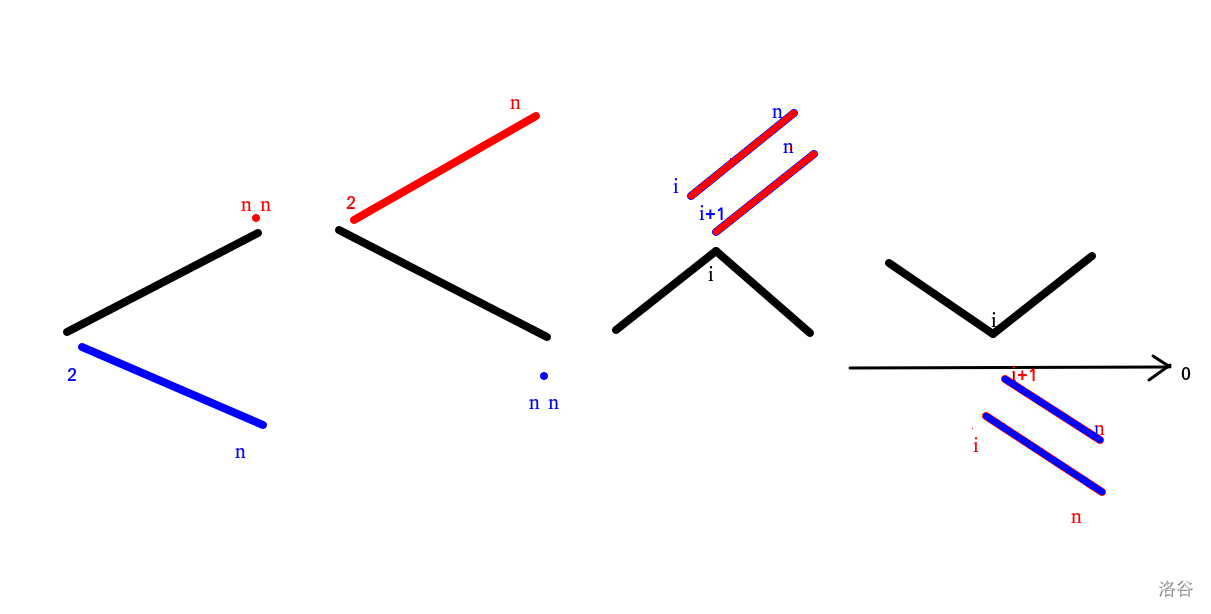
然后跟这题 类似的,我们发现构造的树为内向树 / 外向树 / 拼起来
然后假如这样的树有 种,此时 Bob 无论怎么选路径都会输,于是答案为
我们先来计数纯向树,设 表示大小为 的树根有 个儿子的方案数,有转移
也就是直接给 送一个大小为 的子树,为了方便我们钦定新树根为标号仅次于 的标号,至于若不是的情况,会在向上合并时被计算到。
然后还是与那题类似的,拼起来的树可能会在中间那条链上被计算多次,于是我们倾定最上面 / 最下面的点为根,开始计数,答案为
# sequence
构造啊… 鸽了